Betting is the simplest abstraction to anything we do with our life. In simple terms, we bet with our time to gain other resources/currencies. Which can be further exchanged for other rewards and outcomes.
“If you must play, decide upon three things at the start: the rules of the game, the stakes, and the quitting time.”
Some wise Chinese Guy
Given that, we have established the need to bet on any decision. Understanding the rules and the stakes is absolutely necessary. This along with stop-loss aka, when to quit, is a necessary part of basic risk management.
Sports betting and poker are some of the most interesting spaces where the basic premises of betting come to the fore.
- Whether to bet or not?
- If betting, how much to stake?
Besides computing this decision over a single bet. We need to manage risk by spreading it over multiple bets over a period of time.
Betting 101
When betting we are taking sides on an event where our payoff would vary depending on the outcome of the event. The fundamental assumption here is that all events are independent of each other. Something true for sports bets, poker but may not hold for business.
- Wager or bet an amount on one of the sides.
- Get the payoff corresponding to our side.
We should take the bet if payoff > wager provided a caveat. Besides ensuring the payoff is positive, we need to make sure, we don’t wager all our assets/bankroll over a single decision or a few decisions.
By taking positive payoff decisions spread over a large sample size. We ensure our expected payoff and the actual payoff over the sample are close to each other.
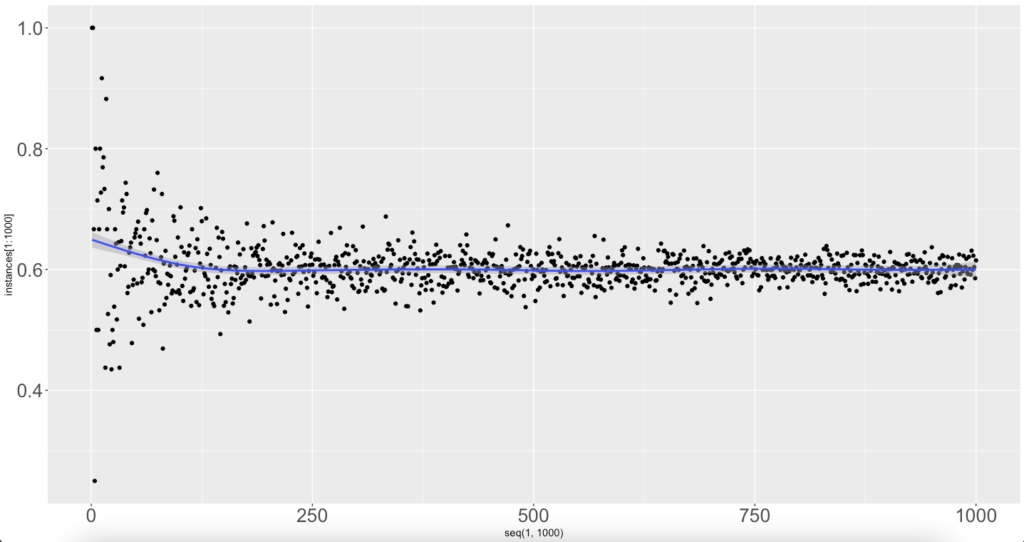
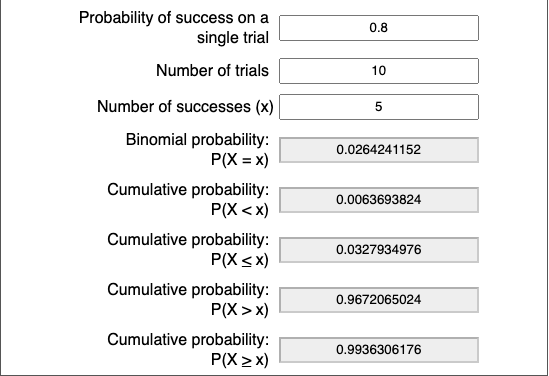
As can be seen over the sample of 1000 events or bets. For a bet with an expected win rate of 60%, our expected win rate over the sample 1000 approaches is close to 0.6.
By consistently making decisions with a positive expectation and doing so over a large sample, our win rate in real life will match our theoretical expectations.
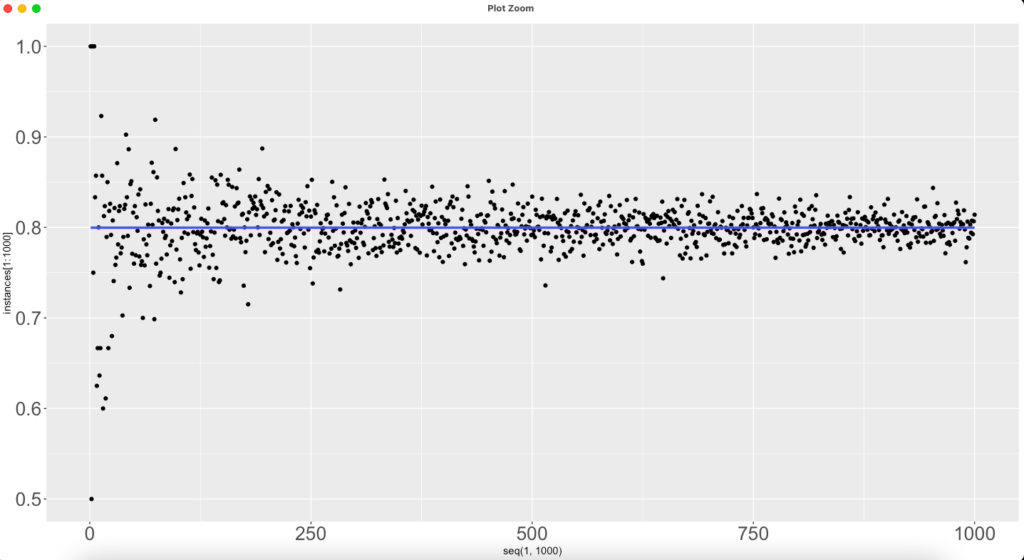
The same graph is a bit different when done with a win rate of 80% or 0.8. We reach the stability of 80% win rate much faster. We are there with a sample of 100 bets.
Volatility/Variance
Though, the expected win rate is the average of all wins. Over a small sample, the actual win rate will defer from our theoretical wins.
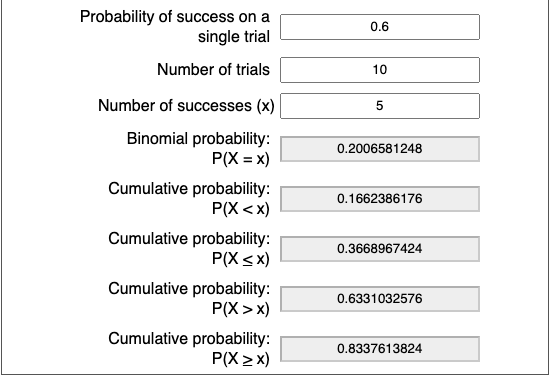
It’s only after 250 bets, does the win rate stabilises enough to reach our expected win rate. This is with a win rate of 0.6 or 60%. The standard deviation will be computed as sqrt(n*P*(1-P))/n. This is derived using the formula for binomial distributions.
- P = 0.6
- n= 1000
Here, n is equivalent to 1000 and the standard deviation of (0.15). Our expectation of at least a 50% win rate from a sample of 10 to 100 changes from 83.% to 98.3%.
50% ensures, we are profitable or have a positive payoff. This will change if we have a rake or vig from the house/bookie. This is the transaction cost for placing the wager and can be assumed to be ~5%.
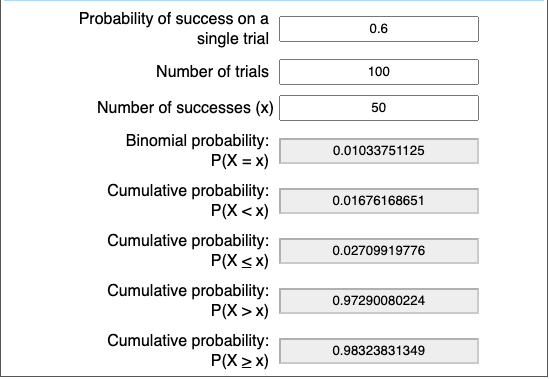
Win a larger win rate of say 0.8 or 80%. Even with 10 as a sample size, we will be profitable in 99% of situations.
Thereby, the variance or volatility of our win rate is a function of both the sample size and just the magnitude of the win rate. To avoid variance, we need to be more conservative about which bets to take (the larger the win rate, the better) and accordingly use an appropriate sample size.
This is one of the most challenging concepts to understand in poker where most decisions are marginal or have a probability of ~60% of happening. But, as can be seen with 60% decisions, we need a huge sample to reach our expected win rate.
Book A Slot
Which bets to take?
We know, we want to make bets with a positive payoff (aka expected outcome greater than wager). We will also understand, the need to spread these bets across a large sample size to be able to realise our expected win rate through the sample.
But when making bets through a bookie or a market as we know it. There are a couple of other considerations to make.
- Rake or Vig (Fee charged by the house/bookie)
- The payoff for taking the bet
The second part is where the discrepancy is. Let’s say your perception of an event happening is 60%. You have an option to make a bet of 100 bucks. You need a payoff of at least (100/0.6) or ~167 to make a profitable trade/bet.
Our perception of an event happening is not the same as what the market deems it to be. If betting on a sports event, the brokerage based on his odds computation and market might allocate the event a probability of 50%. Accordingly, the payoff from him will be 100/0.5 or ~200 minus Vig. This is a bet, we should take because we have a better payoff than the 167 we need.
Capital Market Analogy
Similarly, when we buy a stock in the market. We are buying the future cashflows of the specific firm. The only way, we make money is when our conviction about the company cash flow is greater than what the market perceives it to be. Similarly, it’s the opposite when we are short of stock. Our conviction is lower than the probability the market is allocating it to the company’s cash flow.
The only caveat is trades or positions where the risk of an event going against us has a high cost such as death. Here, while on an expected basis, it does not make sense to take insurance, it works from a risk management point of view. The probability of ruin is very low but the cost of not protecting against it is very high. These are other bets, we should take when the absolute loss because of the downside is very high.
How much to bet ?
Post the decision to take a bet, the other question is how much to bet. How big or small?
In a perfectly liquid market such large betting sites on popular games such as soccer, cricket, stock market etc. We have the ability to size the bet as much as we need.
This does not hold true for poker, where we should not bet more than 1% of our bankroll on any single bet/hand. This is to manage and spread the bets. Even within each hand, we should bet when P*B-Pot_Size > 0 where P is the probability of winning and B is the best size.
In fact, based on the plot for a 60% win rate. We should be looking to make at least 250 bets to realise our theoretical win rate. If we assume, we are taking 80% bets. We should be fine with even 100 bets.
In such events, we have the upper limit of 1-2.5% of our bankroll or book size so that we don’t risk too much in a single trade/bet/hand. Besides that, another consideration for the bet size is the size of the outcome.
Another alternate way to bet is to use the Kelly criterion for bet sizing where we take the concept of positive payoff a little bit forward.
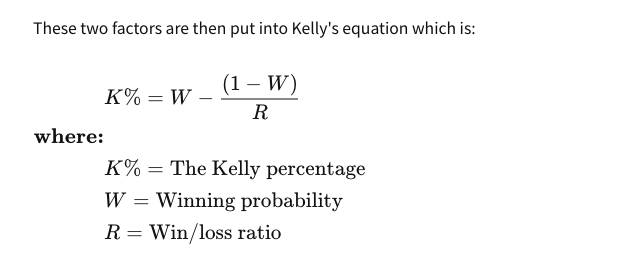
R is the ratio between the average size of the winning amount upon the size of the average loss amount. It’s one more popular way to size the bets.
In poker though, due to the imperfect information nature of the game, a large bet size can be used to represent a larger probability of winning than the actual hand. Popularly, also known as the bluff.
Conclusion
In short, betting has 3 parts to it, whether to bet or not. If yes, how much can we bet optimally? And finally depending upon the risk management and win-rate deciding, capping the risk per each bet.

